Variace bez opakování

1. Počítáme počet různých vlajek sestavených ze 3 svislých pruhů:

Přepis řešení:

Doplňujeme barvy na tři různá místa na vlajce, vybíráme tedy 3 různé barvy z pěti celkem:

  1. 2. 3. →   _ _ _

Na první místo vybíráme 1 z 5 barev, máme tedy 5 různých možností:

  $5$ _ _

Na druhé místo vybíráme už jen ze 4 barev, protože jednu barvu jsme již použili a barvy se nemohou opakovat:

  $5$ $4$ _

Na třetí místo vybíráme už jen ze 3 barev, protože 2 barvy jsme již použili a barvy se nemohou opakovat:

  $5$ $4$ $3$

Výsledek: $5 \cdot 4 \cdot 3 = 60 $.

kombinatorické pravidlo součinu

variace vlajek

2. Úlohu si rozdělíme na tři situace: žlutý pruh bude vlevo nebo uprostřed nebo vpravo na vlajce:

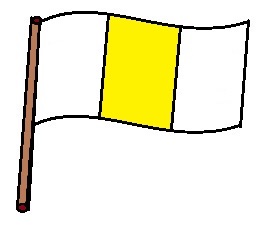
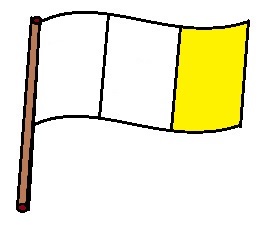
Ž _ _                         _ Ž _                         _ _ Ž

Umístění žluté barvy tímto máme určené. Na toto místo máme pouze jednu možnost výběru barvy = žlutou:

$ 1 $ _ _                         _ $ 1 $ _                         _ _ $ 1 $

Poté nám zůstanou 4 barvy, kterými můžeme obarvit další pruh. Po obarvení tohoto pruhu nám zůstanou 3 barvy na poslední pruh:

$ 1 \ \ 4 \ \ 3 $                       $\ 4 \ \ 1 \ \ 3 $                       $\ 4 \ \ 3 \ \ 1 $

Jednotlivé možnosti:
  $1 \cdot 4 \cdot 3 = 12$,
  $4 \cdot 1 \cdot 3 = 12$,
  $4 \cdot 3 \cdot 1 = 12$.

Máme 3 disjunktní skupiny vlajek, počet vlajek s jedním žlutým pruhem je proto podle pravidla součtu :
  $12 + 12 + 12 = 36$.

3. Nemá červený pruh, počet barev na vlajku je tedy 4:
  $4 \cdot 3 \cdot 2 = 24$.

1. $8$ mužů $+ \ 5$ žen $= 13 $ lidí celkem.
   Předseda Místopředseda Účetní Trenér = P   M   Ú   T   →   _   _   _   _
   Pro výběr předsedy máme 13 možností, poté pro místopředsedu 12 možností, potom pro účetního 11 možností a nakonec pro trenéra 10 možností.
   Výsledek:$ 13 \cdot 12 \cdot 11 \cdot 10 = 17160$.
2. Příklad si rozdělíme na 2 různé situace:
   I. P-muž a M-žena:

   Na místo předsedy vybíráme jednoho z osmi mužů, na místo místopředsedy jednu z pěti žen:
   $8 \ 5 $ _ _
   Zbývá $7$ mužů $+ \ 4$ ženy $= 11 $.
   $ 8 \cdot 5 \cdot 11 \cdot 10 = 4400$.

   II. P-žena a M-muž:
   $5 \ 8 $ _ _
   Zbývají $4$ ženy $+ \ 7$ mužů $= 11 $.
   $ 5 \cdot 8 \cdot 11 \cdot 10 = 4400$.

   Výsledek: $ 4400 + 4400 = 8800$.

3. Nyní musíme uvažovat zvlášť situace, kdy žena je na místě P nebo M nebo Ú nebo T:
   P-žena: $ 5 \cdot 8 \cdot 7 \cdot 6 = 1680$,
   M-žena: $ 8 \cdot 5 \cdot 7 \cdot 6 = 1680$,
   Ú-žena: $ 8 \cdot 7 \cdot 5 \cdot 6 = 1680$,
   T-žena: $ 8 \cdot 7 \cdot 6 \cdot 5 = 1680$,
   $1680 + 1680 + 1680 + 1680 = 6720 $.

A) Úlohu si rozdělíme na 4 různé situace:

1. Výběr čtyřciferných čísel.
2. Výběr tříciferných čísel.
3. Výběr dvouciferných čísel.
4. Výběr jednociferných čísel.

1. Máme čtyři cifry: _ _ _ _
   Na první z nich můžeme umístit čísla: 1, 2, 3, 4, 5, 6, 7, 8, 9. Celkem 9 číslic. (Proč ne nulu? Čísla mají být čtyřciferné.)
   $9$ _ _ _
   Na druhé místo už můžeme umístit i nulu: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Celkem 10 číslic a odečítáme jednu číslici, kterou jsme již vybrali:
   $9$ $9$ _ _
   Na třetí místo: 10 číslic mínus 2 z předchozích výběrů:
   $9$ $9$ $8$ _
   Jako poslední cifru můžeme zvolit opět jednu z 10 číslic mínus 3 z předchozích výběrů:
   $9$ $9$ $8$ $7$
   Celkově: $9 \cdot 9 \cdot 8 \cdot 7 = 4536$.
2. Pro tříciferná čísla analogicky: $9 \cdot 9 \cdot 8 = 648$.
3. Pro dvouciferná čísla analogicky: $9 \cdot 9 = 81$.
4. Jednociferných přirozených čísel je: $9$.

B) Postup řešení je podobný jako v úloze A). Rozdíl bude pro výpočet čtyřciferných čísel.
Na prvním místě mohou být číslice: 1, 2, 3, 4, 5. Celkem 5 číslic.
$5 \cdot 9 \cdot 8 \cdot 7 = 2520$
Počet všech nejvýše čtyřciferných přirozených čísel menších než 6000 je: $2520 + 648 + 81 + 9 = 3258 $.

Mirek si chce vytvořit vlastní vlajku. Chtěl by, aby byla složena ze tří různobarevných svislých pruhů. K dispozici má látky 5 různých barev – fialovou, červenou, modrou, zelenou a žlutou.

Určete, kolik různých vlajek si může Mirek sestavit.

Řešení:

Sportovní klub Komárov vybírá osoby na pozice předsedy, místopředsedy, účetního a trenéra. K dispozici má 8 uchazečů a 5 uchazeček. Určete:

Kolika způsoby z nich lze vybrat tyto funkcionáře?

Řešení:

A) $11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 = 332640 \qquad [=V(6,11)] $.

B) $10 \cdot 1 \cdot 9 \cdot 8 \cdot 7 \cdot 6 = 30240 $.

Označme si číslice:
S-sudá číslice nebo nula, L-lichá číslice, Č-libovolná číslice:

  S   S   S   L   L   Č

  $ 5 \cdot 4 \cdot 3 \cdot 5 \cdot 4 \cdot (2+3) = 6000 $.

1. $ 23 \cdot 22 \cdot 21 \cdot 20 = 212520 \qquad [V(4,23)] $.
2. $ 7 \cdot 6 \cdot 21 \cdot 20 = 17640 $.
3. $ 7 \cdot 6 \cdot 16 \cdot 15 = 10080 $.

1. Počet různých vlajek, které lze sestavit, je: $5 \cdot 4 \cdot 3 = 60 [=V(3,5)]$, což je více než je počet dětí ($45<60 $), proto je možné, aby si každé dítě vytvořilo svou originální vlajku.

2. Prostřední pruh má barvu určenou (= 1 možnost), na ostatní zbývají 4 barvy:
         $4 \cdot 1 \cdot 3 = 12$.
3. Můžeme počítat dvěma způsoby:

   A) Můžeme od počtu všech vlajek odečíst ty, které mají prostřední barvu červenou.
         Počet všech vlajek $5 \cdot 4 \cdot 3 = 60$.
         Počet vlajek s červenou uprostřed $4 \cdot 1 \cdot 3 = 12$.
       Vlajky bez prostředního pruhu červeného: $60 - 12 = 48$.

   B) Máme obarvit 3 pruhy na vlajce:
         _ $\ $ _ $\ $ _
       Začneme od prostředního pruhu. Na něj máme pouze 4 barvy (červenou nechceme):
         _ $\ \ 4 \ \ $ _
       Teď už můžeme použít i červenou barvu, celkem je tedy 5 barev mínus ta barva, kterou už jsme vybrali pro prostřední pruh. Dostáváme:
         $4 \cdot 4 \cdot 3 = 48$.

Počet takových pěticiferných čísel je: $ 9 \cdot 9 \cdot 8 \cdot 7 \cdot 6 = 27216$.

Dělitelných pěti jsou čísla, jejichž poslední cifra je: $ 0$ nebo $ 5$.
Poslední cifra je $0$: $ 9 \cdot 8 \cdot 7 \cdot 6 \cdot 1 = 3024 $, poslední cifra je $5$: $ 8 \cdot 8 \cdot 7 \cdot 6 \cdot 1 = 2688 $, celkem $3024 + 2688 = 5712$.

Takových nejvýše čtyřciferných čísel je: $ 6 \cdot 5 \cdot 4 \cdot 3 + 6 \cdot 5 \cdot 4 + 6 \cdot 5 + 6 = 516. [= V(4,6) + V(3,6) + V(2,6)+V(1,6)] $

Sudých: poslední cifra je 2, 4 nebo 6: $ 5 \cdot 4 \cdot 3 \cdot 3 + 5 \cdot 4 \cdot 3 + 5 \cdot 3 + 3 = 258$.
V druhém případě jsme si mohli počítání ulehčit, všech čísel sestavených z číslic 2, 4, 5, 6, 7, 9 je 516, a jelikož je přesně polovina z číslic 2, 4, 5, 6, 7, 9 sudá, proto také v polovině všech možností bude poslední cifra sudá: $516/2=258$.

$ 16 \cdot 15 \cdot 14 = 3360 \qquad [=V(3,16)]$

Takových čtyřciferných čísel je: $ 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120. \qquad [=V(4,5)]$

Dělitelných pěti: poslední cifra je "5": $ 4 \cdot 3 \cdot 2 \cdot 1 \cdot 1 = 24 $.

Lichých: poslední cifra je "1, 3 nebo 5": $ 4 \cdot 3 \cdot 2 \cdot 1 \cdot 3 = 72 $.

Počet různých svíček je: $ 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 = 6720. \qquad [=V(5,8)] $

S nejvyšším pruhem modrým a nejnižším fialovým či naopak je : $ 2 \cdot 6 \cdot 5 \cdot 4 \cdot 1 = 240 $.

Prostřední 3 barvy jsou červená, oranžová a žlutá: $ 8 \cdot 3 \cdot 2 \cdot 1 \cdot 7 = 336 $.