Princip inkluze a exkluze
Jedná se o další kombinatorické pravidlo, blízké pravidlu součtu.
Pokud se vrátíme k pravidlu součtu, vzpomeneme si, že v příkladech bylo důležité,
aby množiny byly konečné a po dvou disjunktní (žádné dvě množiny neměly žádný společný prvek).
Jak se dá počet prvků sjednocení množin určit, i v případě,
kdy množiny jsou stále konečné ale nejsou po dvou disjunktní,
nám právě prozradí tento princip inkluze a exkluze (neboli slučování a vylučování).
Řešené příklady
Příklad 1 - Turnaje
V Husovicích se konal fotbalový a volejbalový turnaj. Na fotbalový turnaj přišlo 35 účastníků,
na volejbalový 32 účastníků. 12 se jich zúčastnilo fotbalového i volejbalového turnaje.
Kolik přišlo sportovců celkem?
Řešení:(skrýt text)
Označme si jednotlivé množiny:
Množina hráčů fotbalu $= F$
Množina hráčů volejbalu $= V$
Množina hráčů obou sportů $= F \cap V$
Množina všech hráčů $= F \cup V$
Pro připomenutí, počet prvků dané množiny $M$ označujeme $|M|$.
Počítáme počet všech sportovců, kteří se zúčastnili obou turnajů:
*Interaktivním obrázkem můžete pohybovat pomocí modrých bodů ve spodní části obrázku anebo kliknutím a
tažením levým tlačítkem myši.
Přepis řešení:
Zajímá nás počet všech hráčů: $F \cup V = \ ?$
V množině hráčů fotbalu jsou i hráči, kteří hráli také volejbal.
A v množině hráčů volejbalu jsou i hráči, kteří hráli také fotbal.
Z toho důvodu, pokud sečteme počet hráčů fotbalu a počet hráčů volejbalu,
přičteme dvakrát počet hráčů obou sportů ($F \cap V$).
Počet všech hráčů tedy obdržíme, pokud sečteme $|F| + |V|$ a jednou odečteme $F \cap V$:
$$ |F \cup V| = |F| + |V| - |F \cap V| $$
Dosazením:
$$ |F \cup V| = 35 + 32 - 12 = 55 $$
Příklad 2 - Cizí jazyky
Na jazykovém gymnáziu si studenti musí vybrat 1, 2 nebo 3 jazyky. Mají na výběr z: angličtiny, němčiny a francouzštiny.
Ve třídě I. A:
- si angličtinu zvolilo 21 studentů, němčinu si zvolilo 16 studentů a francouzštinu si zvolilo 14 studentů.
- angličtinu a němčinu má 9 studentů, angličtinu a francouzštinu má 8 studentů, němčinu a francouzštinu má 7 studentů.
- všechny tři jazyky si vybrali 3 studenti.
Kolik je ve třídě studentů?
Řešení:(skrýt text)
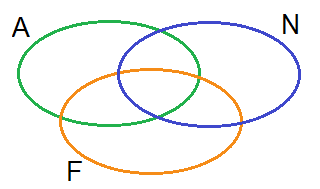
Označme si jednotlivé množiny:
Množina studentů, kteří si zvolili angličtinu $= A$
Množina studentů, kteří si zvolili němčinu $= N$
Množina studentů, kteří si zvolili francouzštinu $= F$
Množina studentů, kteří si zvolili angličtinu i němčinu $= A \cap N$
Množina studentů, kteří si zvolili angličtinu i francouzštinu $= A \cap F$
Množina studentů, kteří si zvolili němčinu i francouzštinu $= N \cap F$
Množina studentů, kteří si zvolili všechny tři jazyky $= A \cap N \cap F$
Množina všech studentů $= A \cup N \cup F$
Zkusíme postupovat stejně jako v předchozím příkladu. Nejprve sečteme počet prvků množin $A, N, F$:
| $ \qquad |A| + |N| + |F| : \qquad $ |
 |
Všimněte si, že vždy přičítáme dvakrát počet prvků v průniku dvou sousedních množin, tj. $|A \cap N|$, $|A \cap F|$, $|N \cap F|$.
A dokonce třikrát počet prvků v průniku všech tří množin, tj. $|A \cap N \cap F|$.
Pomůže nám odečíst počet prvků v jednotlivých průnicích dvou sousedních množin $|A \cap N|$, $|A \cap F|$, $|N \cap F|$?

Pomůže, ale uvědomme si, že s tímto odčítáním odečteme také třikrát počet prvků v průniku všech tří množin, tj. $|A \cap N \cap F|$.
Nejprve jsme ho třikrát přičetli, poté třikrát odečetli, musíme proto ještě jednou přičíst $|A \cap N \cap F|$.
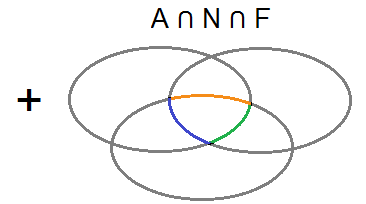
Počet všech studentů v I. A je:
$|A \cup N \cup F| = |A| + |N| + |F| - |A \cap N| - |A \cap F| - |N \cap F| + |A \cap N \cap F|$.
Dosazením:
$|A \cup N \cup F| = 21 + 16 + 14 - 9 - 8 - 7 + 3 = 30$.
Princip inkluze a exkluze
Věta:
Nechť $M_1, M_2, \ldots , M_n $ jsou konečné množiny. Pak platí:
$|M_1 \cup M_2 \cup \ldots \cup M_n| = |M_1| + |M_2| + \ldots |M_n| - $
$\phantom{|M_1 \cup M_2 \cup \ldots \cup M_n| =} - |M_1 \cap M_2| - |M_1 \cap M_3| - \ldots - |M_{n-1} \cap M_n| +$
$\phantom{|M_1 \cup M_2 \cup \ldots \cup M_n| =} + |M_1 \cap M_2 \cap M_3| + \ldots + |M_{n-2} \cap M_{n-1} \cap M_n| -$
$\phantom{|M_1 \cup M_2 \cup \ldots \cup M_n| =} \ldots $
$\phantom{|M_1 \cup M_2 \cup \ldots \cup M_n| =} + (-1)^{n+1} \cdot |M_1 \cap M_2 \cap \ldots \cap M_n| = $
$\phantom{|M_1 \cup M_2 \cup \ldots \cup M_n| =} = \sum (-1)^{r+1} |M_{j_1} \cup M_{j_2} \cup \ldots \cup M_{j_r}|, $
kde se sčítá přes všechny neprázdné podmnožiny $\{j_1, j_2, \ldots, j_r\}$ indexové množiny $\{1, 2, \ldots, n\}$. Součet jsme uspořádali tak,
že na $i$-tém řádku jsou zapsány sčítance odpovídající $i$-prvkovým podmnožinám, je tam tedy $\dbinom{n}{i}$ sčítanců.
Celkový počet sčítanců na pravé straně vzorce je zřejmě $2^n -1$.
Důkaz:(zobrazit text)
Zvolme libovolný prvek $m \in M_1 \cup M_2 \cup \ldots \cup M_n$ a označme $M_{k_1}, M_{k_2}, \ldots, M_{k_s} $ právě ty z uvažovaných $n$ množin,
v nichž prvek $m$ leží ($ s \in \{1, 2, \ldots, n \}$). Zkoumejme, ve kterých množinách typu $ M_{j_1} \cap M_{j_2} \cap \ldots \cap M_{j_r} $ je prvek
$m$ obsažen — zřejmě právě v těch, pro které platí
$$ \emptyset \neq \{j_1, j_2, \ldots, j_r\} \subseteq \{k_1, k_2, \ldots, k_s\}. $$
Pro každé $ r \in \{1, 2, \ldots, s \}$ je tedy prvek $m$ započten v právě $\dbinom{s}{r}$ sčítancích typu $|M_{j_1} \cap M_{j_2} \cap \ldots \cap M_{j_r}|$,
pro $r>s$ pak v žádném. Proto celkový příspěvek prvku $m$ k pravé straně vzorce je
$$ \dbinom{s}{1} - \dbinom{s}{2} + \ldots + (-1)^{s+1} \dbinom{s}{s} = 1 $$
podle identity níže. Na levé straně vzorce je prvek $m$ ovšem započten také právě jednou. Tím je důkaz tvrzení ukončen; zpřesnili jsme v něm názornou
myšlenku, která k odvození vzorce vede: v součtu $|M_1| + |M_2| + \ldots |M_n|$ jsou započteny právě jednou ty prvky, které leží v právě jedné z množin $M_i$;
ty prvky, které leží zároveň v několika množinách, jsou zde započteny vícekrát. Odečteme-li $\sum|M_i \cap M_j|$, uvedeme na pravou míru ty prvky, které leží
právě ve dvou množinách, přitom počty prvků patřících do aspoň tří množin jsou redukovány příliš. To se pro ty prvky, které patří do právě tří množin napraví
přičtením součtu $\sum|M_i \cap M_j \cap M_k|$ atd.
Identita:
Pro $n \geq 1$ platí:
$$ \dbinom{n}{0} - \dbinom{n}{1} + \dbinom{n}{2} - \dbinom{n}{3} + \ldots + (-1)^{n} \dbinom{n}{n} = 0. $$
Příklady k procvičení
Příklad 1
Ve zverimexu mají 15 zvířat, jenž žerou rostlinnou stravu, a 9 zvířat, jenž žerou maso. 5 z těchto zvířat jsou všežravci.
Kolik zvířat mají ve zverimexu?
Řešení: (zobrazit text)
Označíme si:
zvířata, jenž žerou rostlinnou stravu $= R$,
zvířata, jenž žerou maso $= M$,
zvířata, která jsou všežravci $= R \cap M$,
všechna zvířata $= R \cup M$.
$ |R \cup M| = |R| + |M| - |R \cap M| = 15 + 9 - 5 = 19 $.
Příklad 2
Dopravní kontrola zjišťovala technický stav brzd a ojetí pneumatik.
Za špatný stav brzd uložila pokutu 15 řidičům, za ojeté pneumatiky uložila pokutu 12 řidičům.
Ze všech 53 kontrolovaných řidičů nezjistila žádnou chybu u 30.
Vypočítejte, kolik řidičů zaplatilo pokutu za oba zmíněné nedostatky svého vozidla, kolik jen za špatný technický stav brzd,
a kolik jen za ojetí pneumatik.
Řešení: (zobrazit text)
Kontrolováno bylo $53$ řidičů. U $30$ aut kontrola nenašla žádnou chybu. Proto počet aut s nějakou závadou je $53-30=23$.
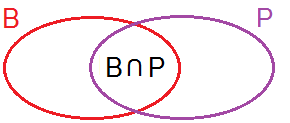
Označíme si:
auta se špatnými brzdami $= B$, $ \qquad |B| = 15$,
auta s ojetými pneumatikami $= P$, $ \qquad |P| = 12$,
auta s nějakou závadou $= B \cup P$, $ \qquad |B \cup P| = 23$,
auta s oběmi závadami $= B \cap P$, $ \qquad |B \cap P| = ?$.
Kolik bylo aut s oběmi závadami?
$$|B \cup P| = |B| + |P| - |B \cap P|$$
$$|B \cap P| = |B| + |P| - |B \cup P| = 15 + 12 - 23 = 4$$
Kolik bylo aut jen se špatnými brzdami?
$$|B| - |B \cap P| = 12 - 4 = 8$$
Kolik bylo aut jen se špatnými pneumatikami?
$$|P| - |B \cap P| = 15 - 4 = 11$$
Příklad 3
Ve vědeckém ústavu pracuje několik lidí, z nichž každý zná alespoň 1 cizí jazyk.
6 ovládá angličtinu, 6 němčinu a 7 francouzštinu.
4 umějí angličtinu i němčinu, 2 angličtinu a francouzštinu, 3 němčinu a francouzštinu.
1 člověk ovládá všechny 3 jazyky.
a) Kolik osob pracuje v ústavu? b) Kolik z nich ovládá pouze angličtinu? c) Kolik z nich umí jen francouzsky?
Řešení: (zobrazit text)

Označíme si:
lidé, kteří umí anglicky $= A$,
lidé, kteří umí německy $= N$,
lidé, kteří umí francouzsky $= F$.
a) $|A| \cup |N| \cup |F| = ?$
$$|A| \cup |N| \cup |F| = |A| + |N| + |F| - |A \cap N| - |A \cap F| - |N \cap F| + |A \cap N \cap F| =$$
$$\phantom{|A| \cup |N| \cup |F|} = 6 + 6 + 7 - 4 - 2 - 3 + 1 = 11$$
b) Z náčrtku vyčteme, že jen angličtinu ovládá:
$$|A| - |A \cap N| - |A \cap F| + |A \cap N \cap F| = 6 - 4 - 2 + 1 = 1$$
c) Z náčrtku vyčteme, že jen francouzsky umí:
$$|F| - |A \cap F| - |N \cap F| + |A \cap N \cap F| = 7 - 2 - 3 + 1 = 3$$
Příklad 4
Z 326 žáků určité školy hraje 92 žáků odbíjenou, 143 žáků nehraje fotbal.
Právě jeden z těchto dvou sportů pěstuje 213 žáků. Kolik žáků hraje fotbal i odbíjenou?
Řešení: (zobrazit text)
Označíme si:
žáci hrající odbíjenou $= O$, $ \qquad |O| = 92$,
žáci hrající fotbal $= F$,
žáci nehrající fotbal ani odbíjenou $= N$,
všichni žáci $= O \cup F \cup N $, $ \qquad |O \cup F \cup N| = 326$,
Jaký je počet žáků hrajících fotbal?
$|F| =$ počet všech žáků - počet žáků nehrajících fotbal $ = 326 - 143 = 183$.
Dále víme, že právě jeden ze dvou sportů pěstuje 213 žáků. Tzn.:
$$ |O| + |F| - 2 \cdot |O \cap F| = 213.$$
Z toho vyplývá, že žáků, kteří hrají fotbal i odbíjenou, je
$$ |O \cap F| = 31.$$
Příklad 5
Personalistka jisté firmy poskytla řediteli následující informaci:
ve firmě pracuje 250 mužů a 200 žen, přitom 160 mužů a 140 žen má vysokoškolské
vzdělání, do práce dojíždí 180 mužů a 100 žen, vysokoškolsky vzdělaných mužů
dojíždí 150 a vysokoškolsky vzdělaných žen 20.
Co z toho může ředitel usoudit?
Řešení: (zobrazit text)
Ve firmě podle údajů pracuje celkem $250+200=450$ lidí.
Kolik z nich je žen bez vysokoškolského vzdělání, které do práce nedojíždějí?
Označme vlastnosti osob:
mužské pohlaví $= M$,
ženské pohlaví $= Z$,
všichni lidé $= M \cup Z = L$,
má vysokoškolské vzdělání $= V$,
nemá vysokoškolské vzdělání $= nV$,
dojíždí do zaměstnání $= D$,
nedojíždí do zaměstnání $= nD$.
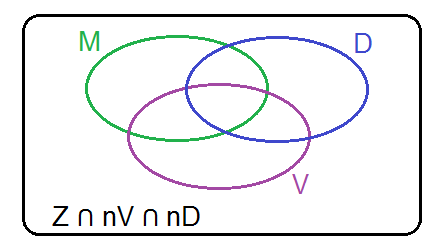
Platí:
$ |M| = 250, $
$ |M \cup Z| = 450,$
$ |V| = 160 + 140 = 300, $
$ |D| = 180 + 100 = 280, $
$ |M \cap V| = 160, $
$ |M \cap D| = 180, $
$ |V \cap D| = 150 + 20 = 170, $
$ |M \cap V \cap D| = 150. $
$$ |Z \cap nV \cap nD| = |L| - |M| - |V| - |D| + |M \cap V| + |M \cap D| + |V \cap D| - |M \cap V \cap D| $$
$$ |Z \cap nV \cap nD| = 450 − 250 − 300 − 280 + 160 + 180 + 170 − 150 = −20 $$
To samozřejmě není možné. Ředitel může usoudit, že personalistka udělala někde chybu.
Příklad 6
Kolik přirozených čísel mezi 1 a 300 je a) dělitelných 3, 5 nebo 7 b) dělitelných 3 a 5, ale nedělitelných 7 c) dělitelných 5, ale ne 3 nebo 7 ?
Řešení: (zobrazit text)
Označíme si:
čísla dělitelná 3 $= A = \{n; 1 \leq n \leq 300, 3| n \}$,
čísla dělitelná 5 $= B = \{n; 1 \leq n \leq 300, 5| n \}$,
čísla dělitelná 7 $= C = \{n; 1 \leq n \leq 300, 7| n \}$,
a) Podle principu inkluze a exkluze platí:
$$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|$$
Při počítání počtu prvků v jednotlivých množinách zaokrouhlujeme u dělení dolů. Zkuste se zamyslet proč?
$ |A| = \lfloor 300 : 3 \rfloor = 100 $
$ |B| = \lfloor 300 : 5 \rfloor = 60 $
$ |C| = \lfloor 300 : 7 \rfloor = 42 $
Co v našem případě znamená $ |A \cap B|$? Čísla dělitelná 3 a zároveň 5, tedy čísla dělitelná 15.
U $ |A \cap C|$, $ |B \cap C|$ a $ |A \cap B \cap C|$ analogicky.
$ |A \cap B| = \lfloor 300 : 15 \rfloor = 20 $
$ |A \cap C| = \lfloor 300 : 21 \rfloor = 14 $
$ |B \cap C| = \lfloor 300 : 35 \rfloor = 8 $
$ |A \cap B \cap C| = \lfloor 300 : 105 \rfloor = 2 $
Dosazením:
$$|A \cup B \cup C| = 100 + 60 + 42 - 20 - 14 - 8 + 2 = 162.$$
b) Hledáme čísla dělitelná 3 a 5, ale nedělitelná 7. Počet prvků této množiny bude roven:
$$|A \cap B| - |A \cap B \cap C| = 20 - 2 = 18.$$
c) Hledáme čísla, která jsou dělitelná 5, ale nejsou dělitelná 3 nebo 7. Počet prvků této množiny bude roven
$$ |B| - |A \cap B| - |B \cap C| + |A \cap B \cap C| = 60 - 20 - 8 + 2 = 34.$$
Příklad 7
Určete počet přirozených čísel mezi 1 a 840, která nejsou dělitelná 6, 10 ani 14.
Řešení: (zobrazit text)
Označíme si:
čísla dělitelná 6 $= A = \{n; 1 \leq n \leq 840, 6| n \}$,
čísla dělitelná 10 $= B = \{n; 1 \leq n \leq 840, 10| n \}$,
čísla dělitelná 14 $= C = \{n; 1 \leq n \leq 840, 14| n \}$,
Podle principu inkluze a exkluze platí:
$$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|$$
Počet přirozených čísel mezi 1 a 840, která nejsou dělitelná 6, 10 ani 14, je:
$$840 - |A \cup B \cup C| $$
Počty prvků v jednotlivých množinách::
$ |A| = \lfloor 840 : 6 \rfloor = 140 $
$ |B| = \lfloor 840 : 10 \rfloor = 84 $
$ |C| = \lfloor 840 : 14 \rfloor = 60 $
V předchozím příkladu jsme jako $ |A \cap B|$ brali čísla dělitelná 3 a zároveň 5, tedy dělitelná 15.
Jednalo se o prvočísla, proto to bylo v pořádku. Nyní chceme znát počet čísel dělitelných
6 a zároveň 10, a to jsou čísla dělitelná právě jejich nejmenším společným násobkem.
$ |A \cap B| = \lfloor 840 : nsn(6,10) \rfloor = 28 $
$ |A \cap C| = \lfloor 840 : nsn(6,14) \rfloor = 20 $
$ |B \cap C| = \lfloor 840 : nsn(10,14) \rfloor = 12 $
$ |A \cap B \cap C| = \lfloor 840 : nsn(6,10,14) \rfloor = 4 $
Dosazením:
$$ 840 - |A \cup B \cup C| = 840 - (140 + 84 + 60 - 28 - 20 - 12 + 4) = 612.$$
Příklad 8
Ve vědeckovýzkumném ústavu pracuje 67 osob; 47 z nich ovládá angličtinu, 35 němčinu a 20 francouzštinu,
23 osob umí anglicky i německy, 12 osob anglicky i francouzsky a 11 osob německy i francouzsky.
Všemi třemi jazyky hovoří 5 osob. Určete, kolik osob neovládá žádný z uvedených tří světových jazyků?
Řešení: (zobrazit text)
$$ |A| \cup |N| \cup |F| = |A| + |N| + |F| - |A \cap N| - |A \cap F| - |N \cap F| + |A \cap N \cap F| =$$
$$ \phantom{|A| \cup |N| \cup |F|} = 47 + 35 + 20 - 23 - 12 - 11 + 5 = 61$$
$$ 67 - |A \cup N \cup F| = 67 - 61 = 6.$$
Příklad 9
Dokažte, že následující zpráva o jednom ročníku jisté základní školy je chybná.
Do ročníku chodí 45 dětí, z toho je 30 chlapců. 30 dětí má dobrý prospěch, z nich je 16 chlapců.
Sportu se věnuje 28 dětí, z toho 18 chlapců a 17 dětí, které mají dobrý prospěch. 15 chlapců má dobrý prospěch a současně sportuje.
Řešení: (zobrazit text)
Označme množinu všech dětí v ročníku $R$, množinu všech chlapců $CH$, množinu všech dětí s dobrým prospěchem $P$
a množinu všech sportovců $S$. Pro množinu všech nesportujících dívek, které nemají dobrý prospěch $D$, platí:
$$ |D| = |R| - |CH \cup P \cup S| = 45-(30+30+28-16-18-17+15) = -7 $$
Což není možné.
Příklad 10
120 studentů absolvovalo zkoušku z matematiky a z fyziky.
82 studentů udělalo zkoušku z matematiky, 85 zkoušku z fyziky, 77 studentů udělalo obě zkoušky.
Určete:
a) Kolik studentů udělalo alespoň jedno zkoušku?
b) Kolik studentů neudělalo zkoušku z matematiky?
c) Kolik studentů neudělalo zkoušku z fyziky?
d) Kolik studentů udělalo zkoušku z matematiky a neudělalo zkoušku z fyziky?
e) Kolik studentů udělalo zkoušku z fyziky a neudělalo zkoušku z matematiky?
Řešení:(zobrazit text)
Označme $S$ množinu všech studentů. $M$ množinu studentů, kteří udělali zkoušku z matematiky. $F$ množinu studentů, kteří udělali zkoušku z fyziky.
Počet prvků jednotlivých množin je: $|S| = 120, |M| = 82, |F| = 85, |M \cap F| = 77$.
a) $|M \cup F| = |M| + |F| - |M \cap F| = 90$
b) $|nM| = |S| - |M| = 38$ (nM - neudělali zkoušku z matematiky)
c) $|nF| = |S| - |F| = 35$ (nF - neudělali zkoušku z fyziky)
d) $|M \cap nF| = |M| - |M \cap F| = 5$
e) $|F \cap nM| = |F| - |M \cap F| = 8$






